一文搞懂考研数列极限问题(概念/计算/证明)史上最强/最全总结

不管本科高数还是考研数学，数列极限问题，看这一篇文章管够，看完还不会做你来找我！

数列极限，是数列和极限两个充满不确定性的概念相混合，容易让人产生摸不着头脑，看到题目就害怕的感觉，本篇文章就按以下目录对这块儿重难点拨云见日，内容循序渐进，越往后越精彩，大家可以自行感受一下！

01 什么是数列
02 数列的极限
03 数列极限的计算(三种类型)
04数列相关证明题(两种类型)

01 什么是数列？(掌握难度：★)

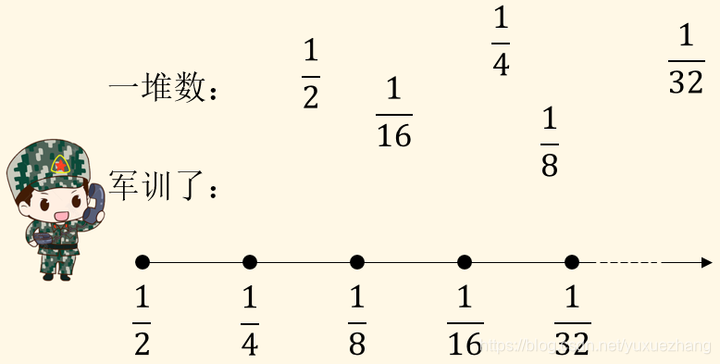
从字面意思就可以看出来：数列数列，就是将数排成队列。详细点来说，就是将一堆数按照某种规律排成一排，p.s.类似军训，教官让我们按照从矮到高(某种规律)排成一排。

这时，有个数在开小差，教官就开始点名了。还记得我们当时军训时教官是怎么点名的么?

“第m排第n列,请出列”——这耳熟能详的语句。

由于我们的数只有一列，所以我们就变成了，“第n个数请出列”。为了描述方便我们用符号 $x_n$ 表示，含义为第n个数，于是就有 $x_1=\frac{1}{2}，x_4=\frac{1}{16}，x_5=\frac{1}{32}$。如果可以用某个含n的式子来表示 $x_n$ ，那么这个式子就叫做这个数列的通项公式，例如本文举例的数列，它的通项公式就是： $x_n=\frac{1}{2^n}$ 。有了它，我们就可以快速get这一列数中的每一个数，是不是很方便。

但是，人总是贪心的。所以一定会有人问：“你不是说每一项你都知道么？那么第无穷项是多少呢？”这个时候就涉及到了数列的极限。

02 数列的极限(掌握难度：★★)

针对刚刚的问题——数列{ $x_n$ }的“无穷项”是多少？即当 $n\to \infty$ 时， $x_n$ 趋近于多少。可见这是一个极限问题，用数学式来表示：

${\lim }_{n\to \infty }{x}_n=?$

上式的结果，有些是可预测的（可计算出结果），有些是不可预测的（结果不确定），如下：

例如：
（1） $(-1{)}^n：-1,1,-1,1,-1,1\dots \dots$

（2） $ln(n):ln1,ln2,ln3，\dots \dots$

（3） $\frac{1}{2^n}：\frac{1}{2}，\frac{1}{4}，\frac{1}{8}，\frac{1}{16}\dots \dots$

数列(1)，在-1和1间摇摆不定，"第无穷项"鬼知道是1还是-1，因此极限不存在；

数列(2)，随n增大， $x_n$ 也无限制地增大，增大到无穷时，无法用一个具体的数来表示，其极限也不存在。对于数列(1)和(2)，我们称其为发散数列，或称这个数列是发散的。

数列(3)，随n增大，每一项的分母都会无限制的增大，进而每一项会越来越小，最终 $n\to \infty ,x_n\to 0(\frac{1}{\infty })$ ，所以此时我们可以预测在“第无穷项”处，数列的值趋近于0，这个时候我们也称数列（3）收敛。

所以可知，当 ${\lim }_{n\to \infty }{x}_n=A$ 的时候，数列的“第无穷项”我们是可以预测出来的，此时这个数列 { x n } \left\{ x_{n} \right\} { xn​} 也是收敛的。最终得到下面的关系：

{ x n } 收敛 ↔ lim ⁡ n → ∞ x n 存在 ↔ lim ⁡ n → ∞ x n = A \left\{ x_{n} \right\}收敛\leftrightarrow\lim_{n \rightarrow \infty}{x_{n}}存在\leftrightarrow\lim_{n\rightarrow \infty}{x_{n}}=A { xn​}收敛↔limn→∞​xn​存在↔limn→∞​xn​=A

极限趋近的数学表达式： $n\to \infty ，x_n\to A$ ，用大白话讲就是：当n趋近无穷大时， $x_n$ 与A的距离越来越近。而衡量两个数的距离远近，用绝对值来表示，就是 $\left|x_n-A\right|$ 。所以该语句套上数学的外衣就是 $n\to \infty$，$|x_n$