一文搞懂积分不等式证明(积分证明题总结笔记3/3)

积分证明题是考研中难度较大的板块，很多学弟学妹们希望我出一篇总结文章，故作本文，希望对大家有所帮助。

本文所涉及题目，均是来自市面上常见题册（李林880，张宇1000题，汤家凤1800等）

由于内容较多，故分为三部分：

等式证明（点击进入）
由积分判断函数零点个数（点击进入）
不等式证明（本文内容）

积分不等式证明：

从市面上常见题册中总结了证明积分不等式的七种常见的方法。汇总如下：

下面主要围绕这七种方法进行最全面的讲解，让同学们全方位搞懂这几个方法。

1.构造函数用单调性做

使用场景：
题目中有单调字眼，或者有 $f^{\prime }(x)＞0$（或$＜0$）时考虑使用

解题步骤：
a.将所证不等式进行移项，并设其中一个字母为 x ，进而构造函数。(注意 x 的范围)
b.将构造的函数进行求导，得到其单调性。(其中有可能会用到中值定理)
c.求解出 x 处于某一范围时，函数的最值，最后变形即证明完成。

例题讲解：
以下面例题为例详细讲解该方法：

设函数时一定要注意函数的定义域。这两道题都是设b为x(当然，如果你想设a为x也是可以的)，所以由 $b\ge a$ 得 $x\ge a$ 。

2.构造二重积分

使用场景：
证明式子中有两函数相乘的积分，且这两个函数在积分区域都是单调时，考虑用该方法。

解题步骤：
设所证明的不等式中含有 ${\int }_a^{b}f(x)g(x)dx$
a.构造式子： $[f(x)-f(y)][g(x)-g(y)]$ (利用单调性判断这个式子和0之间的大小关系)
b.积分：在区域 D = { ( x , y ) ∣ a ≤ x ≤ b , a ≤ y ≤ b } D=\left\{ (x,y)|a\leq x\leq b, a\leq y \leq b\right\} D={(x,y)∣a≤x≤b,a≤y≤b} 上积分
c.化简得证

例题讲解：
用下面例题详细讲解该方法：

3.利用图像解决

使用场景：
题目条件中有 $f(x),f^{\prime \prime }(x)$ 与0之间的关系。并且所证式子中有 ${\int }_a^{b}f(x)dx$ ，考虑使用。
这里其实还有一个隐藏要求：小题！因为大题用图像判断没法写过程。

解题步骤：
a.画出对应式子所表示的面积
b.比较面积大小，并判断对应式子的大小，继而得证

例题讲解：
用下面例题详细讲解该方法：

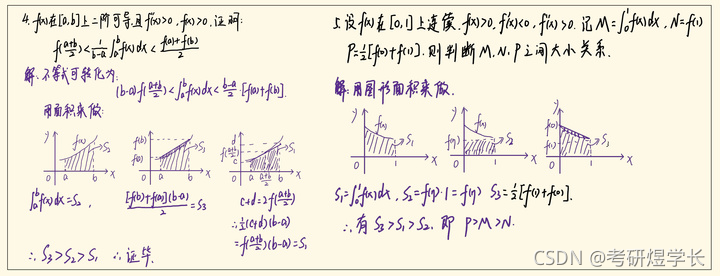
该类型题目最有难度的就是如何表达式子所代表的面积。这需要大家的积累：
例如：看到两个函数值相加再乘某个东西，就要想到会不会是某梯形的面积。

4.分部积分

使用场景：
不等式有 ${\int }_a^b{u}^{(k)}vdx$ 和 $M{\int }_a^{b}udx$ ，其中： ${\max }_{[a,b]}|v^{(k)}|=M$ ，考虑使用。
注：常见的 $u^{(k)}=1$ ，并且有时题目会将 ${\int }_a^{b}udx$ 算出结果，进而 $M{\int }_a^{b}udx$ 转变为一个常数乘以 M 。

解题步骤：
a.分部积分，次数由证明式子决定
b.利用不等式： $|{\int }_a^b\Delta dx|\le {\int }_a^b|\Delta |dx$ 放缩
c.化简得证

例题讲解：
以下面例题为例详细讲解该方法：

分部积分的功效其实和泰勒展开类似，建立起函数和若干阶导数之间的关系。在本题中就是建立起 $f,f^{\prime },f^{\prime \prime }$ 之间的关系（这也决定了要用两次分部积分）。然后利用不等式将 $f^{\prime \prime }$ 和所给的最大值建立联系，最终解决本题。
同时，本题就是对应前面所说的，将 ${\int }_a^{b}udx$ 算出结果，进而转变为一个常数乘以 M 。

5.利用牛顿-莱布尼茨公式

使用场景：
积分不等式中函数的最高阶导数在积分内部时考虑使用
例如：不等式中含有 $f,f^{\prime },f^{\prime \prime }$ ，其中最高阶导数是 $f^{\prime \prime }$ 。因此当这个不等式中有形如 ${\int }_a^b{f}^{\prime \prime }(x)dx$ 或者 ${\int }_a^b|f^{\prime \prime }(x)|dx$ 时，可以考虑使用。

例题讲解

本题所证明不等式中含有 $f$ 和 $f^{\prime }$ ,最高阶导数为 $f^{\prime }$ 。而其在积分内部: ${\int }_a^b|f^{\prime }(x)|dx$ ，所以考虑使用牛顿-莱布尼茨解决。

6.柯西不等式

使用场景：
含有某函数平方积分时考虑使用。
公式为： ${\int }_a^b{f}^2(x)dx{\int }_a^b{g}^2(x)dx\ge [{\int }_a^{b}f(x)g(x)dx{]}^2$

例题讲解：

柯西不等式的功效说白了就是去除积分号里面的平方。对于本题而言就是把 ${\int }_0^1{f}^{\prime 2}(x)dx$ 里面的平方去除，然后建立起 ${\int }_0^1{f}^{\prime }(x)dx$ 和条件 $f(1)-f(0)$ 之间的关系，如何建立？牛顿-莱布尼茨公式为你效劳。

从这两题中我们可以发现两个特点：
1.都是设柯西不等式中的 $g(x)=1$，这也是常见的设法。
2.都用了牛顿-莱布尼茨公式。
细细观察这两题，都满足：积分不等式中函数的最高阶导数在积分内部。所以都使用了牛顿-莱布尼茨公式也不意外。

7.泰勒展开(包含拉格朗日)

使用场景：
题目中含有 m a x { ∣ Δ ∣ } max\left\{ |\Delta| \right\} max{∣Δ∣}，或者题目中含有二阶导时，可以尝试使用。
拉格朗日由于可以看成是泰勒展开的特殊形式($n=0$)，因此也被归为此种方法。

泰勒展开方法总结：
用泰勒展开证明积分不等式的方法多种多样，所以我在这里总结几种练习册上常用的，如下：

当然做题仅靠这些是不够的，还需记住以下几个常见不等式：

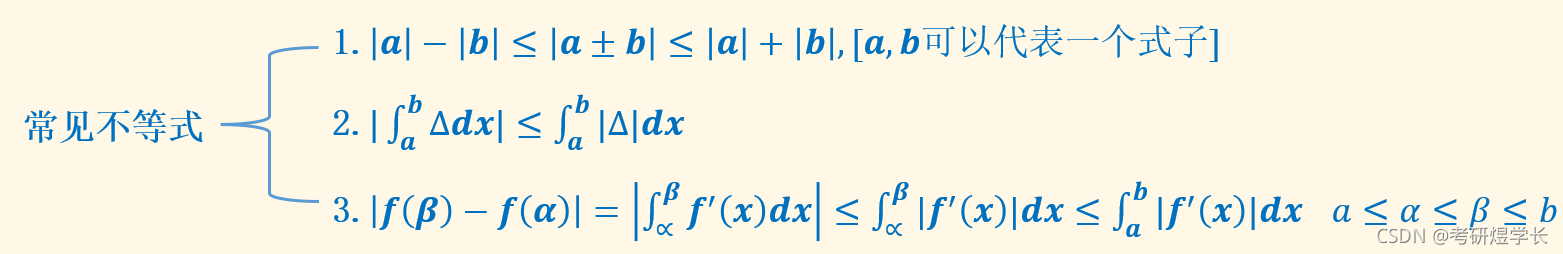
例题讲解：
泰勒展开类型1：

在区域中点展开有个好处，即积分之后可以去除与所证明不等式无关的 $f^{\prime }$ 。

泰勒展开类型2：
已知两个端点的值，证明积分和一阶导最大值之间的关系。
证明流程：在区间端点处展开 $\to$ 分段积分合并$\to$利用不等式得结果

这种类型的题目在练习册中见的还蛮多的，所以可以将其进行拓展，如下图：

本题就是对上面那个进行了拓展（其中 $a=0,b=1$ 就变成了上面那道题）

泰勒展开类型3：
本类题可以通过设变限积分为某个函数，去除不等式中的积分号，从而使积分不等式转变为普通的不等式，此时再按照泰勒展开证明不等式的套路来即可。

泰勒展开类型4：

本题所证不等式中最高阶导数（ $f^{\prime \prime }$ ）在积分内部，因此考虑使用牛顿-莱布尼茨。尝试之后发现直接使用不行。但是，我们可以利用最开始讲的常见不等式的第三条进行解决。

到此结束~
我是煜神学长，考研我们一起加油！！！

关注TB店铺：KY煜神思维导图，了解考研数学提分利器思维导图