电力电子领域逆变器曲面边界控制研究及其归一化几何推导方法资源-CSDN文库

版权申诉

13 浏览量 2025-01-14 21:02:21 上传评论收藏 2.09MB PDF 举报

资源推荐

资源详情

资源评论

IEEE TRANSACTIONS ON POWER ELECTRONICS, VOL. 23, NO. 6, NOVEMBER 2008 2915

Advanced Boundary Control of Inverters

Using the Natural Switching Surface:

Normalized Geometrical Derivation

Martin Ordonez, Student Member, IEEE, John E. Quaicoe, Senior Member, IEEE, and Mohammad Tariq Iqbal

Abstract—A curved switching surface (SS) for inverters control

with superior characteristics is geometrically derived in this pa-

per. In order to avoid inaccuracies introduced by simpliﬁcation or

assumptions, the analysis is performed entirely using a versatile

geometrical method in the normalized domain. Unlike previous

approaches, both the output voltage and the capacitor current are

considered as varying references to establish a more accurate con-

trol law with enhanced performance. The proposed normalization

technique provides remarkable insight into the behavior of system,

the leading to a pure geometrical treatment that is general and ap-

plicable to any possible inverter. As a result of a rigorous analysis,

a control law for inverters deﬁned as natural SS is proposed and

thoroughly characterized. In addition to the enhanced dynamic re-

sponse, ﬁxed-frequency operation is one of the key features of the

proposed control scheme. In order to formally demonstrate ﬁxed-

frequency operation, a transformation from the natural SS to its

pulsewidth modulation (PWM) equivalent is performed, revealing

duality between boundary control using curved SS and traditional

PWM. This is a signiﬁcant advancement toward the uniﬁcation

and understanding of traditional modulation against modulation

produced by curved SSs. Finally, an additional novel concept is

explored: operation in mixed monopolar and bipolar mode using

the natural SS. This new mixed operating mode overcomes physical

limitations of the inverter structure in monopolar mode around the

region of zero voltage cross (both the problem identiﬁcation and so-

lution are investigated). Experimental results of a 1.5-kVA inverter

operating at ﬁxed moderate frequency are presented to validate the

natural SS performance, illustrate the beneﬁts of the normalization

technique, and demonstrate the monopolar and mixed operating

mode.

Index Terms—Boundary control, curved, inverter, nonlinear

control, switching surface.

I. INTRODUCTION

UCK-DERIVED inverters, full- and half-bridge topolo-

gies, can be classiﬁed as simple cases of a variable structure

system that can be controlled by boundary or geometric con-

trol [1]–[6]. Among boundary controllers, a sliding mode using

linear control laws and a hysteresis band has been investigated

extensively for both dc–dc buck converters and buck-derived

inverters [5]–[14]. Under this control scheme, the state vari-

Manuscript received November 27, 2007; revised February 20, 2008. First

published November 17, 2008; current version published December 9, 2008.

This work was supported by the Natural Sciences and Engineering Research

Council (NSERC), Canada. Recommended for publication by Associate Editor

J. Espinoza.

The authors are with the Faculty of Engineering and Applied Science, Memo-

rial University of Newfoundland, St. John’s, NL A1B 3X5, Canada (e-mail:

mordonez@ieee.org).

Color versions of one or more of the ﬁgures in this paper are available online

at http://ieeexplore.ieee.org.

Digital Object Identiﬁer 10.1109/TPEL.2008.2005378

ables of the system experience fast natural transitions until the

switching surface (SS) is intersected. Thereafter, a sliding-mode

regime around the SS surface forces continuous changes in the

structure of the converter, producing a reduction in the order

of the system. The slow sliding transition (compared to natural

trajectories) ﬁnally arrives at the target operating point. In order

to improve the dynamic response of buck-derived converters,

curved SSs were proposed to avoid sliding and reach the target

operating point faster (by extending the natural transitions).

A particular case of a second-order SS with enhanced dy-

namic response was derived using capacitor charge balance

equations [15], and compared to the ﬁrst-order SS. Subse-

quently, the natural unloaded SS for dc–dc buck converters

was investigated [16], showing improved transient character-

istics (compared to the second-order SS), especially under light

loading conditions. Recently, a higher order SS was presented

to control full-bridge inverters, which was also derived from ca-

pacitor charge balance equations (like the second-order SS) [17].

In this case, the resistive loading condition was considered as

part of the control law, and averaging assumptions were made

in the formulation of the control law.

By careful evaluation of previous work in the area, a number

of fundamental technical problems were identiﬁed.

1) Derivation of control laws using time-domain averag-

ing assumptions lead to formulation inaccuracies. This

has particular impact on the large-signal operation of the

system.

2) The concept of target operating point is applicable only

to dc–dc converters [16]. Since inverters have a sinusoidal

reference signal, the control objective must be treated as

a target operating trajectory, rather than a target operat-

ing point. This aspect also affects the performance of the

control law.

3) The set of rules or management rules for a given curved

SS will play an important role in achieving optimal re-

sults. For example, even though good dynamic behavior is

shown in [17], the system operates with variable switch-

ing frequency due to the management rules. This produces

undesirable electromagnetic perturbations and additional

ﬁltering problems.

4) The involvement of unknown parameters in the control

law must be avoided (i.e., load resistance in [17]). The

objective of a good control scheme is to compensate for

unknown disturbances.

This paper proposes a number of advanced technical solu-

tions to overcome the limitations described earlier. In order to

2916 IEEE TRANSACTIONS ON POWER ELECTRONICS, VOL. 23, NO. 6, NOVEMBER 2008

avoid inaccuracies introduced by simpliﬁcation or assumptions,

the analysis presented in this paper is performed entirely us-

ing a versatile geometrical analysis. Both the output voltage

and the capacitor current are considered as varying references

to establish a more accurate control law with enhanced perfor-

mance. This concept is deﬁned as a target operating trajectory

instead of target operating point. The proposed normalization

technique provides remarkable insight into the behavior of the

inverters, leading to a pure geometrical treatment that is gen-

eral and applicable to any possible inverter. As a result of the

analysis, a control law for inverters deﬁned as natural SS is

proposed and characterized thoroughly. In addition to the en-

hanced dynamic response, ﬁxed-frequency operation is one of

the key features of the proposed control scheme. In order to

formally demonstrate ﬁxed-frequency operation, a transforma-

tion from the natural SS to its pulsewidth modulation (PWM)

equivalent is performed, revealing duality between boundary

control using curved SS and traditional PWM. This is a signif-

icant advancement toward the uniﬁcation and understanding of

traditional modulation against modulation produced by curved

SSs. Finally, an additional novel concept is explored: operation

in a mixed monopolar and bipolar mode using the natural SS.

This new mixed operating mode overcomes physical limitations

of the inverter structure in the monopolar mode around the re-

gion of zero-voltage cross (both the problem identiﬁcation and

solutions are investigated). Experimental results of a 1.5-kVA

inverter operating at ﬁxed moderate frequency are presented to

validate the natural SS performance, illustrate the beneﬁts of

the normalization technique, and demonstrate the monopolar

and mixed operating mode.

II. N

ORMALIZATION OF FULL-BRIDGE INVERTER TOPOLOGY

Prior to the normalization, the analysis starts with a basic

review of a full-bridge inverter with its possible structures, as

shown in Figs. 1 and 2. For simplicity, the parasitic elements

(e.g., switch voltage drop, capacitor equivalent series resistance

(ESR), etc.) are neglected. The inverter can be represented with

a system of differential equations as follows:

= i

− i

(1)

= v

u − v

. (2)

As can be seen in Fig. 1, the voltage applied to the output

ﬁlter can take two active levels, v

and −v

, depending on

the state of the switches and the direction of the current. This

is represented in (2) by u =1and u = −1 for v

and −v

respectively. A short circuit or zero state can also be applied to

the output ﬁlter when u =0in (2), as depicted in Fig. 2. In or-

der to simplify the mathematical representation of the inverter,

a normalization technique is employed to disengage some of the

parameters of the converter. The normalization is performed by

using the ﬁlter characteristic impedance Z



L/C, natural

frequency f

=1/T

=1/(2π

√

LC), and the converter refer-

Fig. 1. Full-bridge inverter structures. (a) v

.(b)−v

applied to the output

ﬁlter.

Fig. 2. Full-bridge inverter structures: short circuit applied to the output ﬁlter.

ence voltage v

as base quantities

(3)

(4)

yielding normalized differential equations

− i

√

(5)

ccn

u − v

√

. (6)

ORDONEZ et al.: ADVANCED BOUNDARY CONTROL OF INVERTERS USING THE NATURAL SS: NORMALIZED GEOMETRICAL DERIVATION 2917

Solving (5) and (6), and performing a change of variable to

obtain time normalization t

= t/T

, a simpliﬁed solution in-

dependent of L and C is obtained.

)=[v

(0) − v

ccn

u] cos (2πt

)

+[i

(0) − i

] sin (2πt

)+v

ccn

u (7)

)=[i

(0) − i

] cos (2πt

)

− [v

(0) − v

ccn

u] sin (2πt

) − i

. (8)

Also, the normalized capacitor current (particularly important

in this paper) is given by

)=−[v

(0) − v

ccn

u]sin(2πt

)

+[i

(0) − i

] cos (2πt

) . (9)

As shown in (7)–(9), the behavior of the converter is mathemat-

ically represented in a normalized time domain (independent

from L and C). This normalized mathematical representation

establishes a number of important relations that will be inves-

tigated to obtain the natural trajectories of the system and a

curved SS for high-performance inverter control.

III. D

ERIVATION OF THE INVERTER NATURAL TRAJECTORIES

This section provides an insightful analysis of the inverter

control objectives. The analysis is presented using a unique nor-

malized graphical representation that is valid for any possible

inverter. Taking advantage of the generality given by the normal-

ized expressions derived in Section II, the natural trajectories

of the inverter toward an arbitrary target operating point are

derived. As will be seen, the ﬁndings provided in this and the

following sections result in signiﬁcant advancements in the area

of inverter boundary control using curved SSs.

In order to successfully derive the desired control law, the

initial conditions i

(0) and v

(0) based on the steady-state

operation of the inverter should be evaluated carefully. Even

though the full-bridge inverter is a buck-derived topology, the

initial conditions in this application vary signiﬁcantly from that

of a buck dc–dc converter. This has notable impact on the math-

ematical derivation of the control law.

First, and unlike its dc–dc counterpart, the inverter deals with

a sinusoidal varying reference with a given amplitude v

and

frequency f

. Second, and not so evident, the ﬁlter capacitor

does not have zero current in steady-state operation. Instead, a

leading sinusoidal current with a ripple waveform is obtained

in steady-state operation. These two waveforms determine the

target operating trajectory i n the inverter as opposed to a single-

target operating point in the dc–dc counterpart.

Both the desired output voltage and capacitor current tar-

get trajectories can be represented in normalized form by the

simple application of the base quantities and time-variable

transformation

)=sin



2πt



(10)

where the peak value of the output voltage v

is used as the

voltage base quantity. The corresponding normalized capacitor

Fig. 3. Inverter-normalized target operating trajectory.

current trajectory is given by

Crn

cos



2πt



. (11)

Solving to eliminate t

and since cos



sin

−1



√

1 − x

,the

target operating trajectory is given by

Crn

/ω

=1 (12)

which represents an ellipse with semiminor axis a and semima-

jor axis b

(x)

(y)

=1. (13)

It should be noted that the ratio between the inverter fundamental

frequency ω

and the ﬁlter natural frequency ω

is a nondimen-

sional quantity. As will be explained, this ratio plays a critical

role in the design of inverters using curved SSs. Fig. 3 shows

a graphical representation (phase plane) of the target operating

trajectory in the normalized inverter.

The following important concepts can be inferred from the

graphical examination of Fig. 3.

1) The normalized rotational speed of the elliptical trajectory

is less than 1 (the ﬁlter natural frequency is generally

greater than the inverter fundamental frequency).

2) The normalized capacitor peak current is equal to the nor-

malized rotational speed.

3) The appearance of the ellipse will approach a circle as ω

approaches ω

Now, the initial conditions can be deduced from (11) and (10)

to satisfy

(0) = v

(14)

(0) − i

= i

Crn

(15)

in which the normalized capacitor current should match the

difference between the normalized output current and induc-

tor current, and the output voltage is equal to the normalized

reference voltage.

Now that the initial conditions have been established suc-

cessfully, the converter natural trajectories that intersect the tar-

get operating trajectory can be derived. By employing a set of

2918 IEEE TRANSACTIONS ON POWER ELECTRONICS, VOL. 23, NO. 6, NOVEMBER 2008

trigonometrical identities

A sin(x)+B cos(x)=



+ B

sin



x + tan

−1





and sin



cos

−1

(x)





1 − x

is eliminated from (7) and (9), yielding a generalized expres-

sion for the converter natural trajectories (transformation from

parametric equations to Cartesian coordinates)

λ = i

− i

Crn

+(v

− v

ccn

− (v

− v

ccn

. (16)

It is important to note that the natural trajectories presented in

(16) are valid for any possible inverter regardless of the ﬁlter

values L, C, output voltage, fundamental frequency, ﬁlter cutoff

frequency, and switching frequency.

The geometrical interpretation of the proposed natural trajec-

tories is described in Section IV. First, the steady-state output

voltage is considered as a simple target operating point where

the capacitor current is equal to zero. Thereafter, a more elabo-

rated description of the operation of the inverter with an actual

target operating trajectory is developed.

IV. G

EOMETRICAL ANALYSIS OF THE NATURAL TRAJECTORIES

The geometrical characteristics of the natural trajectories are

initially evaluated using two simple target operating points. In

this particular case, v

=1combined with i

Crn

=0and v

−1 with i

Crn

=0are employed. This, in combination with the

switch control action (u =1, u =0, and u = −1), results in

ﬁve possible natural trajectories

= i

+(v

− v

ccn

)

− (1 − v

ccn

)

=0 (17)

= i

+ v

− 1=0 (18)

= i

+(v

+ v

ccn

)

− (−1+v

ccn

)

=0 (19)

= i

+(v

+ v

ccn

)

− (1 + v

ccn

)

=0 (20)

= i

+(v

− v

ccn

)

− (−1 − v

ccn

)

=0. (21)

All ﬁve natural trajectories represent a perfect circle in a phase-

plane plot (normalized output voltage versus normalized capac-

itor current) that can alternatively be described by

(x − x

)

+ y

= r

(22)

where x = v

, x

= v

ccn

u, y = i

, and r = v

− v

ccn

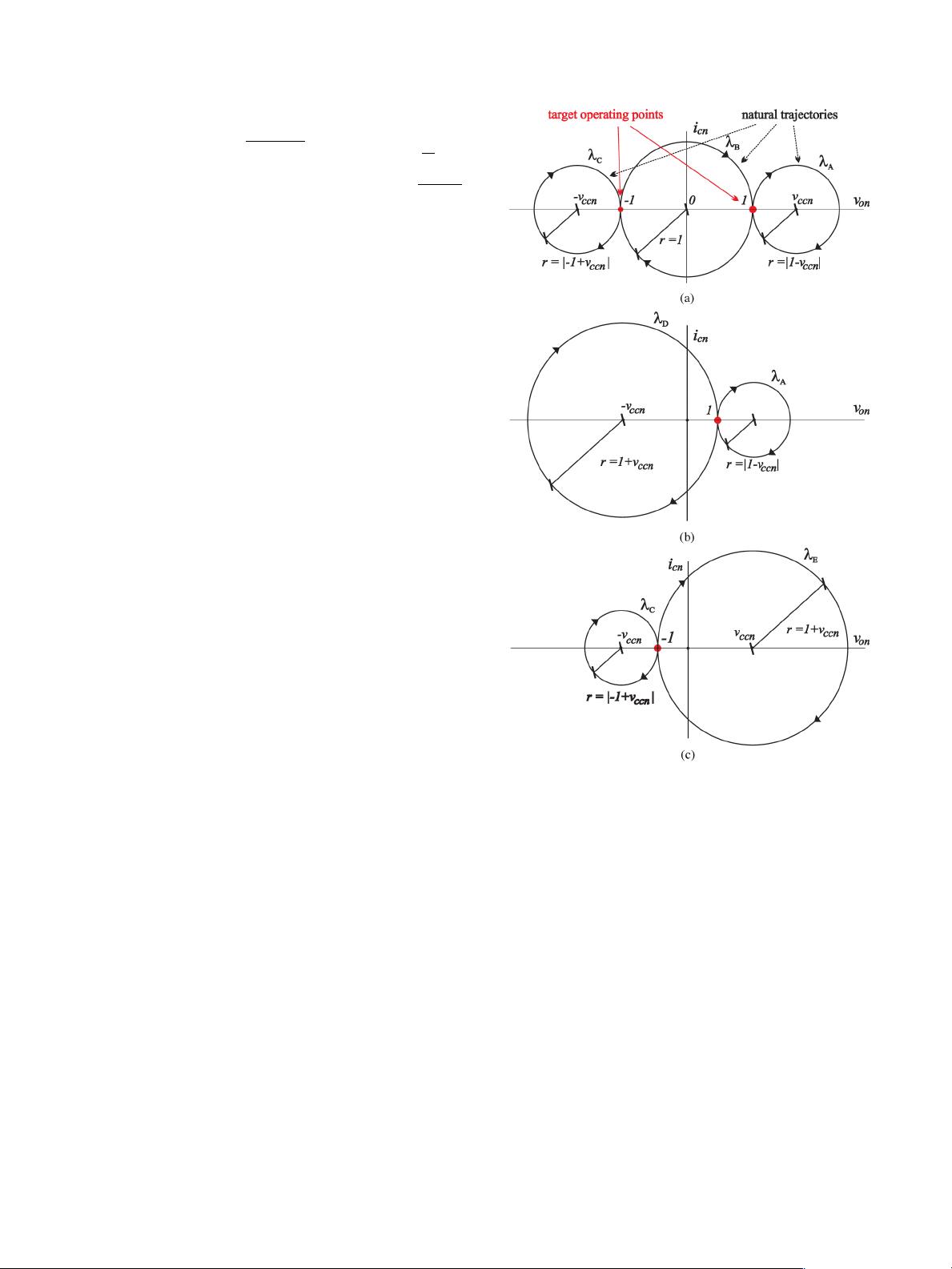
The natural trajectories are shown in Fig. 4 with remarkable

simplicity. The dots located at v

=1and v

= −1 indicate

the target operating points for a positive and negative voltage

reference, respectively. As can be seen in Fig. 4(a) and (b), the

target operating point v

=1can be reached with four natural

trajectories. Also, the target operating point v

= −1 can be

reached by four circles, as indicated in Fig. 4(a) and (c). A

simple yet powerful conclusion is obtained by visual inspection

of Fig. 4: the inverter can be operated in unipolar mode (λ

, and λ

) or bipolar mode (λ

, λ

, and λ

) to achieve

any desired operating point. This provides a unique modulation

feature that will be investigated in Section V.

The analysis is extended to a target operating trajectory in-

stead of a single operating point. By combining the target oper-

Fig. 4. Inverter natural trajectories for v

=1, v

= −1,andi

Crn

=0.

(a) Unipolar mode of operation. (b) and (c) Bipolar mode of operation.

ating trajectory (see Fig. 3), (16), and the switch control action

(u =1, u =0, and u = −1), three possible generalized natural

trajectories are obtained as follows:

= i

− i

Crn

+(v

− v

ccn

)

− (v

− v

ccn

)

(23)

= i

− i

Crn

+(v

)

− (v

)

(24)

= i

− i

Crn

+(v

+ v

ccn

)

− (v

+ v

ccn

)

. (25)

As can be inferred from (23)–(25), the natural trajectories con-

template any arbitrary target point or target trajectory deﬁned

by the reference output voltage v

and reference capacitor cur-

rent i

Crn

. In the particular case of an inverter, v

and i

Crn

are deﬁned by (10) and (11). In order to illustrate this concept,

Fig. 5 shows a conceptual graphical representation of the natural

trajectories of (23)–(25) that intersect an arbitrary point within

the inverter desired operating trajectory.

剩余15页未读，继续阅读

评论收藏

内容反馈

版权申诉

pk_xz123456

粉丝: 2968
资源: 4150

电力电子领域逆变器曲面边界控制研究及其归一化几何推导方法

LCL型并网逆变器的控制技术,lcl型并网逆变器的控制技术 pdf,TEXT

单相逆变器重复控制和双环控制技术研究.pdf

电力电子逆变器课件

Matlab simulink电力电子无源逆变器的控制仿真

5.单相逆变器并网_闭环,单相逆变器双闭环控制,matlab

三相电压型逆变器电压闭环控制simulink仿真,三相逆变器simulink模型,C,C++

单相逆变器的PI控制

基于simulink的并网逆变器PQ控制仿真(1)_逆变器_逆变器pq控制_逆变器控制_电源电流环三电平并网模型_并网仿真

DSP28335控制单相逆变器双闭环控制程序

并网逆变器，功率控制，有功和无功解耦，dq轴分别控制

单相光伏并网逆变器的控制方法综述与PI控制参数整定的探讨.docx

三相DC-AC逆变器模型推导

LCL型并网逆变器的控制技术.pdf

三相电压型逆变器电压闭环控制simulink仿真模型

电力电子simulink仿真源文件SPWM 逆变器等simulink仿真文件25个合集.zip

高频开关型逆变器及其并联并网技术.rar

matlab电力系统仿真-LCL滤波器并网逆变器双闭环控制系统仿真

单相逆变器simulink仿真,simulink整流逆变器仿真,matlab

逆变器控制软件.zip_SPWM STM32 电机_stm32 三相逆变_stm32 逆变器_三相逆变 spwm_逆变电机

三电平逆变器的SVPWM控制策略研究及其在APF中的应用

PWM 逆变器双环控制技术研究

正弦逆变器控制软件设计.PDF

Matlab 电力电子 RCD负载 逆变器 比例谐振控制

2019.1.5电流电压双闭环的PI单相逆变器仿真.rar_DSP 逆变器_DSP逆变器_dsp 逆变器闭环_dsp单相逆变_

最新资源

Matlab 电力电子 RCD负载逆变器比例谐振控制