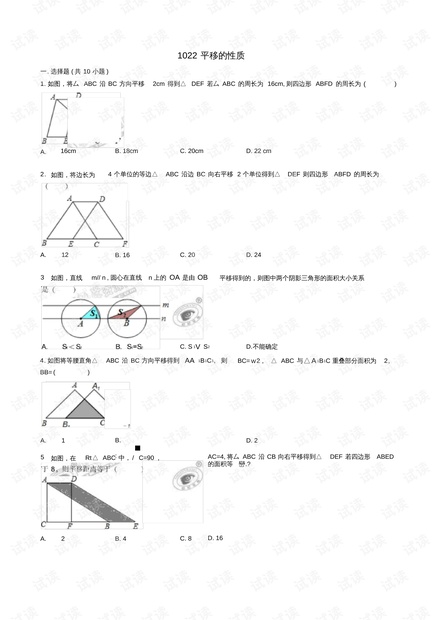
在初中数学教学中,平移作为几何变换的一个基础知识点,具有重要的地位和作用。华东师大版的七年级数学下册教材,在10.2章节专门讨论了平移,并在第二课时深入探讨了平移的性质以及相关的同步跟踪训练,旨在帮助学生通过练习题的形式,巩固和深化对平移概念的理解和应用。本章不仅涉及图形平移的基本性质,还包括了周长与面积保持不变、平移距离的确定方法等关键点,对于培养学生的几何思维和解决实际问题能力有着重要作用。
平移的性质是本章的核心内容。所谓平移,是指在平面内将一个图形沿着一定的方向和距离移动,但不改变图形的形状和大小。在平移过程中,每个点移动的距离和方向都是相同的,这导致了平移后的图形与原图形全等。这一性质的理解,对于解决后续的相关问题至关重要。例如,在解决涉及等腰直角三角形或等边三角形平移问题时,我们能够清楚地知道,无论图形如何平移,其边长、角度甚至面积都保持不变。这种不变性是分析平移问题的基础,也是解决相关几何问题的关键线索。
周长与面积在平移中的保持不变是本章的另一个重点。当一个图形进行平移时,它的周长和面积都不会发生变化。这一性质在解答题目时经常被应用,尤其在涉及到复杂图形的平移时,理解这一性质能够帮助我们快速地确定答案。例如,在一个四边形平移的情况下,其周长等于原三角形周长加上平移的总距离。同样,面积保持不变的原则可用于验证图形平移的正确性。
除此之外,平移距离的确定也是平移问题中经常遇到的一个问题。通常,我们可以通过比较平移前后对应点的坐标来确定平移的具体距离,或者通过测量图形上特定线段的长度变化来确定。在一些题目中,平移距离甚至直接以图形的边长作为单位来描述,比如“平移2个单位”或“平移边BC长度的两倍”。这种描述方式要求学生在掌握基本概念的同时,能够灵活运用所学知识解决实际问题。
平移在几何图形中的应用是多样化的,本章还涉及了重叠部分的处理、矩形平移的特点以及角度保持不变等。例如,在处理具有重叠部分的图形时,重叠部分可以用来辅助判断平移距离或者用于计算图形的面积。矩形平移后,其对角线长度不变,而周长的计算则需要将各个小矩形的周长进行累加。在所有这些情况中,了解平移的性质能够为学生提供解题的思路和方法。
为了让学生更好地掌握平移的性质,并将其应用到实际的几何问题中,同步跟踪训练的设计至关重要。这种训练通常包括填空题、选择题、解答题等多种题型,每一种题型都旨在考察学生对平移概念的理解程度以及解决问题的能力。通过大量的练习,学生能够加深对平移性质的认识,并在解答过程中培养严谨的逻辑思维和空间想象能力。
本章节通过平移的性质、周长和面积的保持、平移距离的确定等知识点,对学生进行了全面的训练和指导,不仅帮助他们掌握了重要的几何概念,而且提高了他们的解题技巧和数学素养。通过这些内容的学习和实践,学生将能够在未来的数学学习和考试中,更加自信和熟练地应用平移的知识点解决复杂的几何问题。