
时域有限差分法对平面 TE 波的
MATLAB 仿真
摘 要
时域有限差分法是由有限差分法发展出来的数值计算方法。自 1966 年 Yee
在其论文中首次提出时域有限差分以来,时域有限差分法在电磁研究领域得到了
广泛的应用。主要有分析辐射条线、微波器件和导行波结构的研究、散射和雷达
截面计算、分析周期结构、电子封装和电磁兼容的分析、核电磁脉冲的传播和散
射以及在地面的反射及对电缆传输线的干扰、微光学元器件中光的传播和衍射特
性等等。
由于电磁场是以场的形态存在的物质,具有独特的研究方法,采取重叠的研
究方法是其重要的特点,即只有理论分析、测量、计算机模拟的结果相互佐证,
才可以认为是获得了正确可信的结论。时域有限差分法就是实现直接对电磁工程
问题进行计算机模拟的基本方法。在近年的研究电磁问题中,许多学者对时域脉
冲源的传播和响应进行了大量的研究,主要是描述物体在瞬态电磁源作用下的理
论。另外,对于物体的电特性,理论上具有几乎所有的频率成分,但实际上,只
有有限的频带内的频率成分在区主要作用。
文中主要谈到了关于高斯制下完全匹配层的差分公式的问题,通过 MATLAB
程序对 TE 波进行了仿真,模拟了高斯制下完全匹配层中磁场分量瞬态分布。得
到了相应的磁场幅值效果图。
关键词:时域有限差分 完全匹配层 MATLAB 磁场幅值效果图


目 录
摘 要 ...............................................................................................................................................1
目 录 ...............................................................................................................................................2
第一章 绪 论 ...............................................................................................................................3
1.1 课题背景与意义 ..................................................................................................................3
1.2 时域有限差分法的发展与应用..........................................................................................3
2.1 Maxwell 方程和 Yee 氏算法...............................................................................................6
2.2 FDTD 的基本差分方程.........................................................................................................8
2.3 时域有限差分法相关技术................................................................................................10
2.3.1 数值稳定性问题 .........................................................................................................10
2.3.2 数值色散 .....................................................................................................................10
2.3.3 离散网格的确定 .........................................................................................................11
2.4 吸收边界条件 ....................................................................................................................11
2.4.1 一阶和二阶近似吸收边界条件 .................................................................................12
2.4.2 二维棱边及角顶点的处理 .........................................................................................15
2.4.3 完全匹配层 .................................................................................................................17
2.5 FDTD 计算所需时间步的估计...........................................................................................21
第三章 MATLAB 的仿真的程序及模拟...................................................................................23
3.1 MATLAB 程序及相应说明...................................................................................................23
3.2 出图及结果 ........................................................................................................................26
3.2.1 程序部分 ......................................................................................................................26
3.2.2 所出的效果图 .............................................................................................................27
第四章 结 论 .............................................................................................................................29
参考文献 .........................................................................................................................................30

第一章 绪 论
1.1 课题背景与意义
20 世纪 60 年代以来,随着计算机技术的发展,一些电磁场的数值计算方法
逐步发展起来,并得到广泛应用,其中主要有:属于频域技术的有限元法
(FEM)、矩量法(MM)和单矩法等;属于时域技术方面的时域有限差分法(FDTD)、
传输线矩阵法(TLM)和时域积分方程法等。此外,还有属于高频技术的几何衍射
理论(GTD)和衍射物理理论(PLD)等。各种方法都具有自己的特点和局限性,在实
际中经常把它们相互配合而形成各种混合方法
[1~2]
。其中 FDTD 是一种已经获得
广泛应用并且有很大发展前景的时域数值计算方法。时域有限差分(FDTD)方法
于 1966 年由 K.S.Yee
[3]
提出并迅速发展,且获得广泛应用。K.S.Yee 用后来被
称作 Yee 氏网格的空间离散方式,把含时间变量的 Maxwell 旋度方程转化为差分
方程,并成功地模拟了电磁脉冲与理想导体作用的时域响应。但是由于当时理论
的不成熟和计算机软硬件条件的限制,该方法并未得到相应的发展。20 世纪 80
年代中期以后,随着上述两个条件限制的逐步解除,FDTD 便凭借其特有的优势
得以迅速发展。它能方便、精确地预测实际工程中的大量复杂电磁问题,应用范
围几乎涉及所有电磁领域,成为电磁工程界和理论界研究的一个热点。目前,FDTD
日趋成熟,并成为分析大部分实际电磁问题的首选方法。
另外,利用矩量法求解电磁场问题时,要用到并失 Green 函数。对于某些问
题,可以找到其解析形式的并失 Green 函数;而对于复杂的问题,很难找到其解
析形式的并失 Green 函数,这样就使得问题无法解决。作为时域分析中的一个重
要数值方法,FDTD 不存在这样的问题。
1.2 时域有限差分法的发展与应用
经过四十多年的发展,FDTD 已发展成为一种成熟的数值计算方法。在发展
过程中,几乎都是围绕几个重要问题展开的,即数值稳定性、计算精度、数值色
散、激励源技术以及开域电磁问题的吸收边界条件等。
数值稳定和计算精度对任何一种数值计算方法都是至关重要的。A.Taylor 和
M.E.Brodwin
[4]
利用本征值方法给出了直角坐标系下 FDTD 的空间步长与时间步
长之间的关系。X.Min 等
[5]
研究了存在边界条件时 FDTD 的稳定性问题。对于数值
色散,与实际的物理色散不同,它是由电磁场量在空间和时间上的对波动方程作
差分近似处理造成的。这种色散引起的误差造成在计算区域内传播的电磁波逐渐
畸变
[6~7]
。K. L. Shlager 等
[8]
比较了二维和三维空间中几种正交网格算法的色散误
差。当采用其他变形或非正交网格时,必须重新分析其数值稳定性和色散特性
[9~11]
,P.Monk 和 E.Suli
[12]
分析了不均匀长方体网格算法的稳定性。
激励源的设计和引入也是 FDTD 的一个重要任务。目前,应用最广泛的激励
源引入技术是总场/散射场体系
[12]
。对于散射问题,通常在 FDTD 计算空间中引
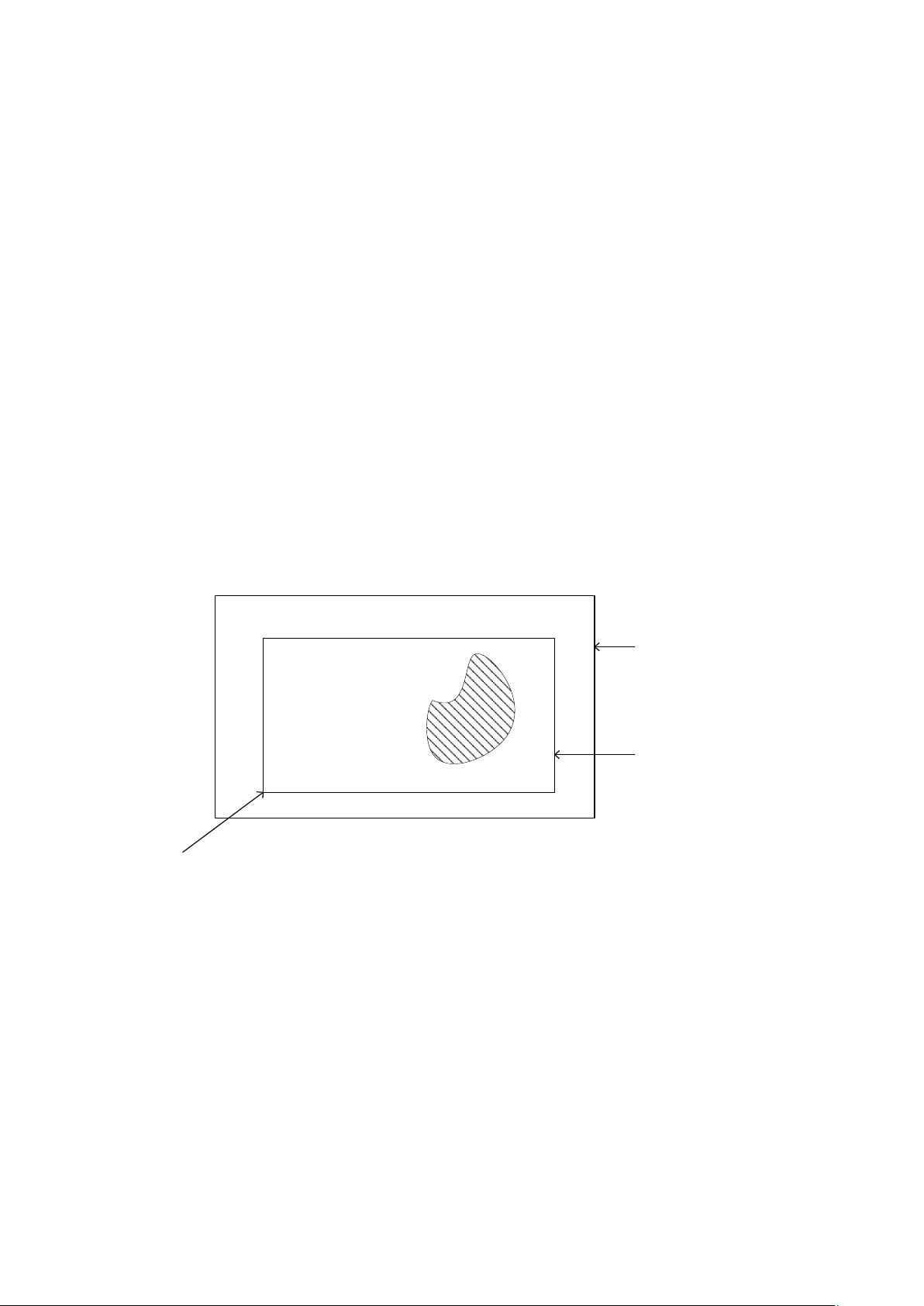
入连接边界,它将整个计算空间划分为内部的总场区和外部的散射场区,如图 1-1。
利用 Huygens 原理,可以在连接边界处引入入射场,使入射场的加入变得简单易
行。
II 散射场区
I 总场区
吸收边界
连接边界
散射体
入射波
图 1-1
开域电磁问题中,为了在有限的计算空间内模拟无限空间中的电磁问题,必
须在计算空间的截断边界处设置吸收边界条件。吸收边界条件从开始简单的插值
边界,已经发展了多种吸收边界条件。在早期得到广泛应用的是 G.Mur
[13]
的一阶
和二阶吸收边界条件,它是基于 B.Engquist 和 A.Majda
[14]
的单向波方程而提出的
差分格式,在 FDTD 仿真区域外边界具有 0.5%到 5%的反射系数。目前应用最广
泛的是 J.P.Berenger
[15-17]
的分裂式完全匹配层,以及 Z.S.Sacks 等
[18]
和




















评论6