对应于小波系数 d
1
、d
2
及 d
3
;尺度空间 V
3
的频带为 0-f/8,对应于尺度系数 a
1
。由此可知,局部放电
超高频信号经过小波多尺度分解,各尺度上信号分量为原始信号在不同频带上的信号分量。
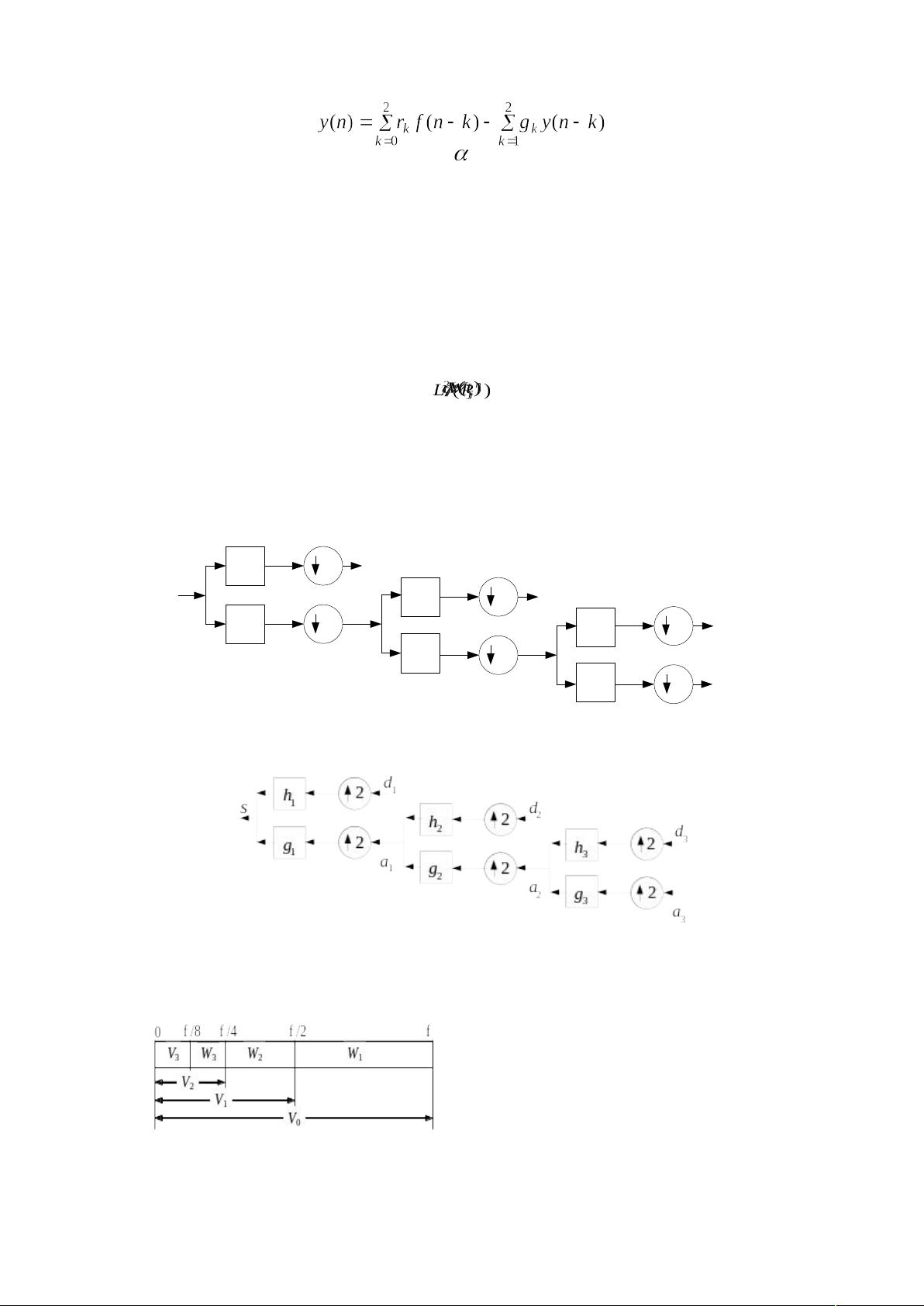
图 3 多尺度分解信号分量频带示意图
给定放电脉冲信号序列 s={s
i
: i=1, 2, , n},小波阈值法去噪可分为以下三个基本步骤:
① 对信号 s 进行离散小波变换,得到小波系数 w
j,k
,k 为第 j 层小波空间的小波系数阶数;
② 各尺度对应的小波系数经过阈值函数处理后,得到估计小波系数 ŵ
j,k
;
③ 采用阈值处理后的小波系数进行离散小波反变换,得到估计信号 ŝ。
在小波阈值法去噪
中,可根据式(11.3-10)作全局阈值估计,即各尺度上小波系数阈值相等,其表达式为:
式中 n 为信号长度。该方法估计的与小波分解的尺度无关,在所
有尺度上,使用同一阈值对小波系数进行收缩处理。如果选择 n 为各尺度上的小波系
数的长度,则成为与尺度相关的小波系数阈值。Donoho 等给出了尺度相关阈值计算
方法:式中为各尺度上的小波系数的长度;,其中 MAD(·)表示取序列的中值;w
j,k
为
各尺度上的小波系数;q 根据经验可在 0.4~1 之间选取,Donoho 等取其为 0.6745。
小波系数阈值化,也称为小波
缩减(Wavelet Shrinkage),主
要分为软阈值法和硬阈值法。
硬阈值法采用阈值化函数 η
h
,仅保留绝对值大于阈值的小波系数,并且被保留的小波系数与原始
系数相同;软阈值法采用阈值化函数 η
s
,对绝对值小于阈值的小波系数值取零,对绝对值大于阈
值的小波系数数值用来缩减。两种阈值化函数如下
这两种方法虽然在实际中得到广泛应用,也取得了较好的效果,但这两种方法本
身有一些潜在的缺点,比如:硬阈值方法中,w
j,k
在处是不连续的,利用 ŵ
j,k
重构所
得信号可能会产生一些振荡;由软阈值方法估计出来的 ŵ
j,k
虽然整体连续性好,但是
当|w
j,k
|>时,ŵ
j,k
与 w
j,k
总存在偏差,直接影响着重构信号与真实信号的逼近程度。
二 典型应用实例
1、局部放电脉冲是一种瞬态信号,可采用指数衰减波形 s
1
和衰减振荡波形 s
2
两种函数模拟,分别
如(1)和(2)式所示。
(1)
(2)
式中, A 为信号幅值系数,
1
和
2
为衰减时间常数,
d
=2f
d
为振荡角频率,
=tg
1
(
d
/
2
)。给定两种局部放电脉冲仿真信号波
形,各参数分别为:A=1,
1
=1×10
-6
s,
2
=1×10
-7
s,f
d
=1MHz。仿真信号采样率为 60Mbps。如果设
定局部放电脉冲幅值为 1,并与幅值为 0.1 的白噪声和幅值为 0.5 的窄带周期干扰(无线电通讯干
扰)信号叠加,窄带周期干扰中包含 100kHz、200kHz、500kHz、700kHz、1.5MHz 等五个频率分
量,幅值比依次为 0.5:0.3:1.0:0.6:0.8。























- 1
- 2
- 3
- 4
前往页