实验内容:
⑴ 用matlab语言代码实现。
⑵ 产生粉红色噪声和高斯色噪声:让高斯白噪声通过低通、带通、高通滤波器中的任意一个就可以产生高斯色噪声。让高斯白噪声通过每倍频程衰减3dB的衰减滤波器的滤波器就可以产生粉红噪声。
⑶ 对粉红色噪声和高斯色噪声进行相关分析和谱分析。计算粉红色噪声、高斯色噪声的均值、均方值、方差、相关函数、概率密度、频谱及功率谱密度、相关函数。
⑷ 所有结果均用图示法来表示,能读出具体值。
色噪声是一种非均匀分布的随机信号,其特点在于不同频率成分的功率不等。相比于白噪声,色噪声在频域内的功率分布具有特定的模式,这使得它在多个领域,如音频工程、通信系统和信号处理中都有重要的应用。本实验主要探讨了色噪声的原理,并提供了使用MATLAB进行实现的方法。
实验目标不仅要求了解随机信号的基本统计特性,如均值、均方值、方差、相关函数、概率密度等,还涉及色噪声的分析方法,特别是通过MATLAB进行仿真实验。色噪声主要包括粉红噪声、高斯色噪声等类型,它们各有特点:
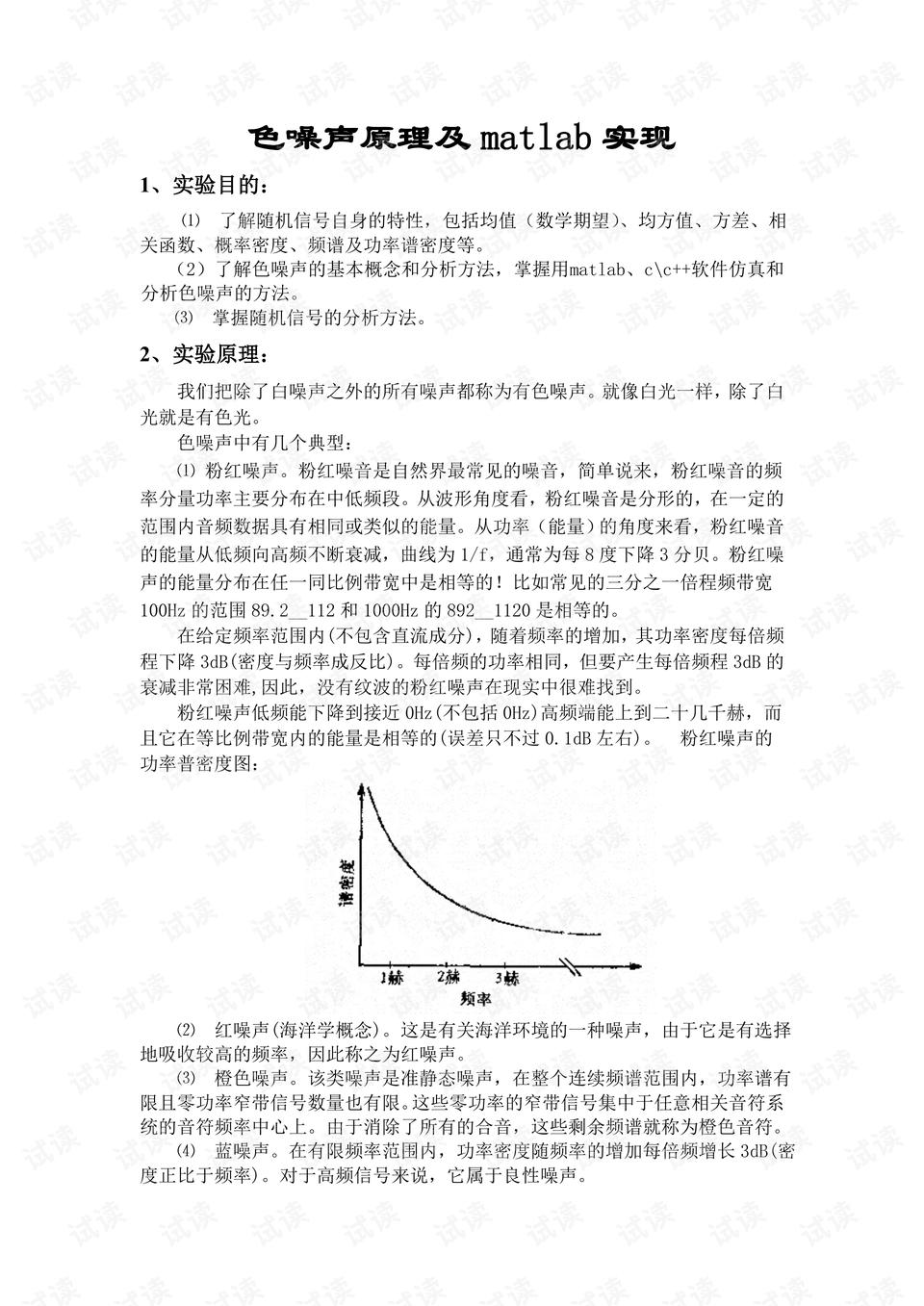
1. **粉红噪声**:粉红噪声是一种在每个八度频率间隔内功率下降3dB的噪声,呈现1/f的功率谱分布。这种噪声在自然环境中广泛存在,其能量在所有频率间隔内相对均衡。粉红噪声的频谱分布使得它在音频领域常被用于测试和校准设备。
2. **高斯色噪声**:由高斯白噪声经过滤波器处理产生,通常通过低通、带通或高通滤波器来改变其频谱特性。高斯色噪声并不具有均匀的功率谱,与白噪声相比,其频率成分更加集中。
实验内容包括:
1. 使用MATLAB或C/C++编程语言,编写和仿真噪声生成程序。
2. 利用滤波器将高斯白噪声转化为高斯色噪声(例如,通过低通滤波器得到的通常是红色噪声)和粉红噪声(通过每倍频程衰减3dB的滤波器)。
3. 对生成的粉红噪声和高斯色噪声进行统计分析和谱分析,计算其均值、方差、相关函数等参数,并绘制概率密度、频谱和功率谱密度图。
4. 结果以图形方式展示,便于直观理解并读取数值。
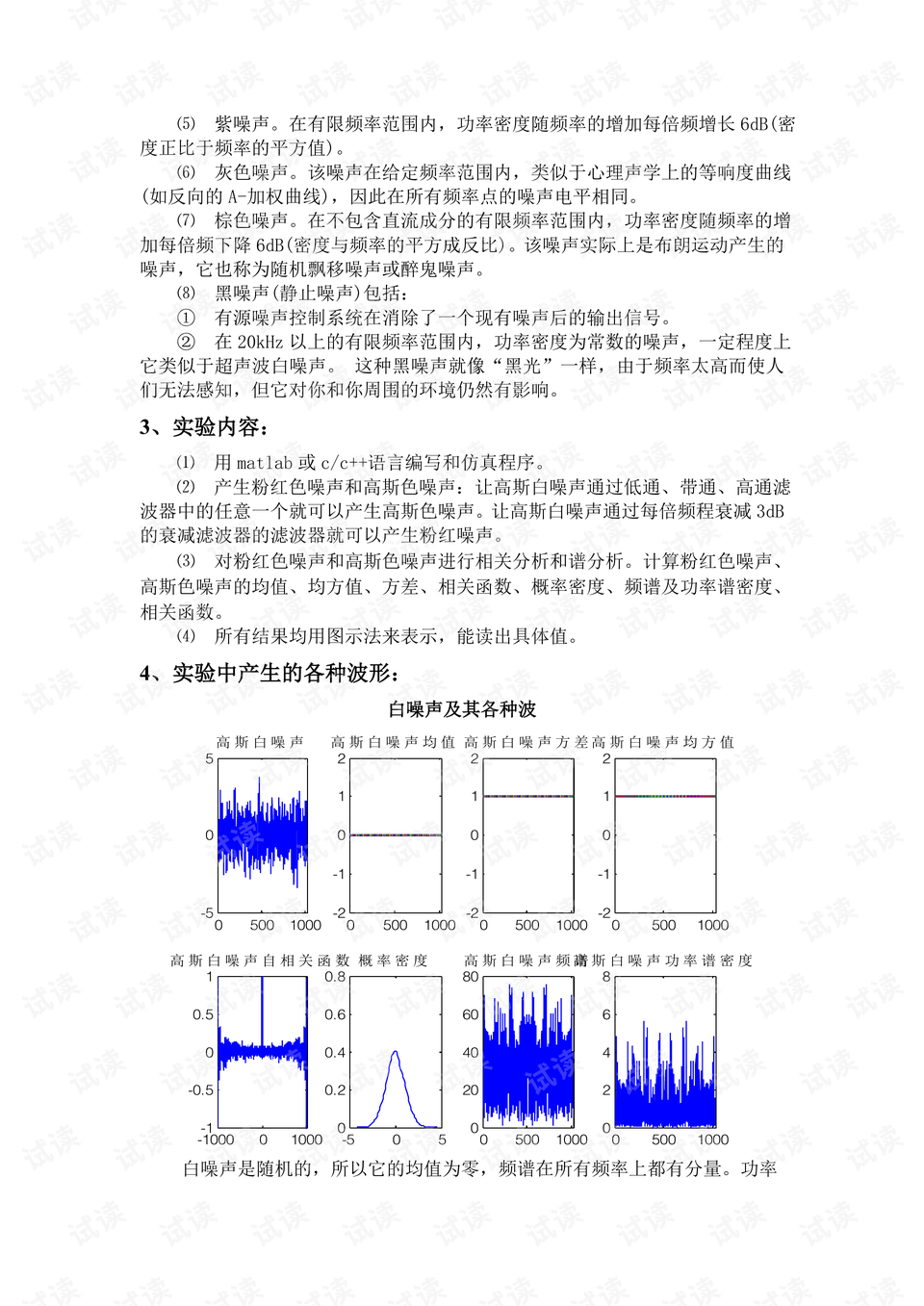
实验过程中会生成不同类型的噪声波形,如白噪声、高斯白噪声、高斯色噪声等。通过观察和分析这些波形的特性,可以深入理解噪声的性质。例如,白噪声的均值为零,频谱在整个频率范围内均匀分布;而高斯色噪声的频谱分布则不均匀,且具有一定的波动,这意味着其均值可能不为零。
这个实验旨在通过MATLAB实践加深对色噪声原理的理解,掌握噪声的分析和生成方法,这对于信号处理和通信系统的设计有着重要的理论和实际意义。通过这样的实验,学习者能够更好地理解和应用随机信号的统计特性,以及在实际问题中如何利用MATLAB工具进行信号分析。